思维碰撞出灵感 在线说题促提高 记凤凰路校区初中部数学中考题说题比赛

4月1日下午，我校初中部数学学科举行了中考题说题比赛，秦紫薇和李久芹两位老师参加比赛，数学组教研组长郭英老师及中学教务主任李少芳老师参与打分。

秦紫薇老师选取了一道单动点问题做为比赛题目。紫薇老师归纳如下：

解决单动点问题一般可归纳为三步完成:第一步设参数，第二步表达关键线段的长度，第三步写成函数或方程的形式。第一步设参数可以从两方面来考虑：第一方面可直接设时间为参数；第二方面可以利用函数关系设动点的横坐标为参数。第二步表达关键线段的长度时需要考虑两点：第一点怎样找到关键线段，也就是哪条线段是关键线段，第二点怎样表达关键线段的长度，我们可以从两个数学角度来考虑：代数和几何。在这个问题上我们可以从第三步确定函数或方程来下手。在代数问题当中，我们更加擅长求的是平行于x轴或者y轴的线段。如果平行于x轴那么横坐标的差的绝对值就是线段的长度；如果平行于y轴那么纵坐标差的绝对值就是线段的长度。当然，单动点问题的本质就是点的运动，在运动当中，涉及到三个量—路程、速度、时间。已走线段的长度就可以用速度乘时间表示，而未走线段的长度可以用总路程减去速度乘时间来表示。单动点问题一般是建立在一次函数，反比例函数，二次函数图像上的，题目花样比较多，但它的过程基本按照这三步来完成的

李久芹老师说的是2019年菏泽中考压轴题。题目如下：

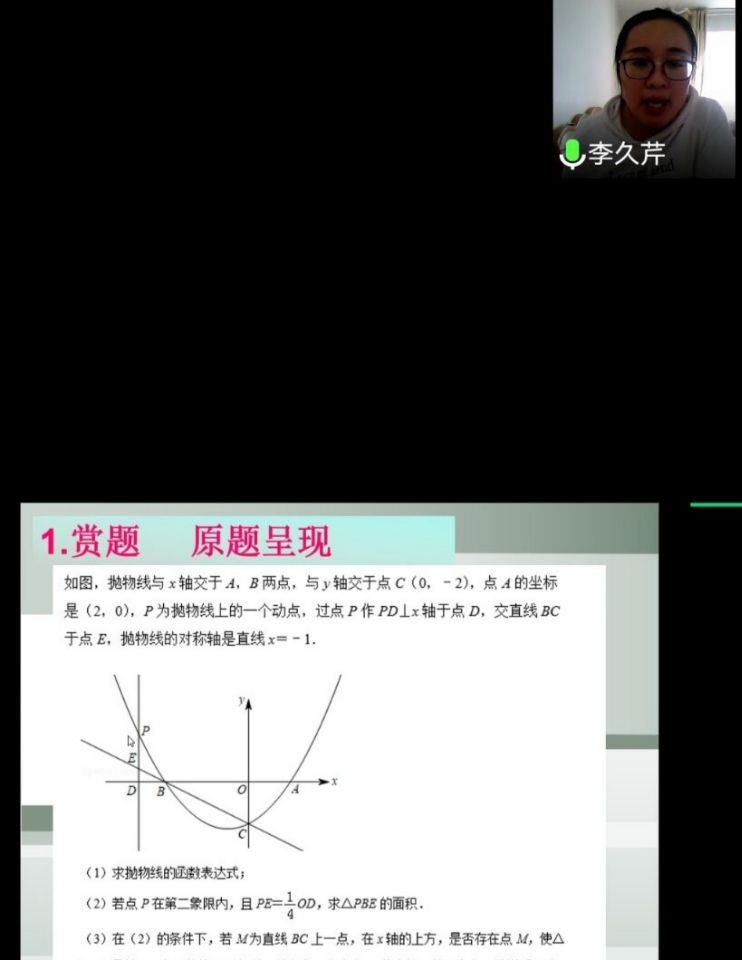
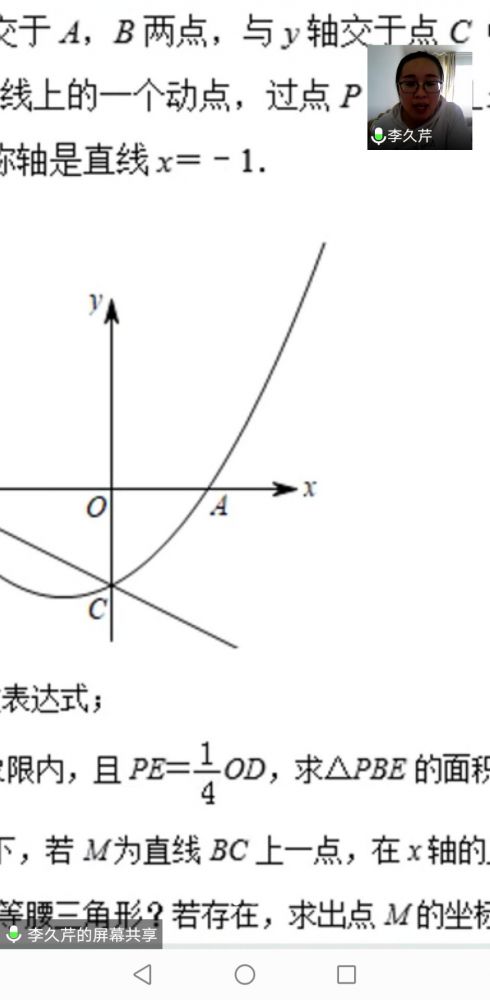
【2019年菏泽中考24题】如图，抛物线与x轴交于A，B两点，与y轴交于点C（0，﹣2），点A的坐标是（2，0），P为抛物线上的一个动点，过点P作PD⊥x轴于点D，交直线BC于点E，抛物线的对称轴是直线x＝﹣1．

（1）求抛物线的函数表达式；

（2）若点P在第二象限内，且PE＝OD，求△PBE的面积．

（3）在（2）的条件下，若M为直线BC上一点，在x轴的上方，是否存在点M，使△BDM是以BD为腰的等腰三角形？若存在，求出点M的坐标；若不存在，请说明理由．

 久芹老师强调：由第（1）问，学生不难得出函数的解析式为y＝x²+x﹣2；；值得注意的是一定要把解析式求对，这里也是考察同学们的计算能力。在这里我们主要分析第（2）问和第（3）问。

首先分析第（2）问中的条件与问题：

条件1：点P在第二象限内；

条件2：PE＝OD；

问题：求△PBE的面积

我们要求三角形的面积，根据S_△PBE＝PE×BD即可求得，求面积关键是求得PE、BD的长度。这就需要设点的坐标，一般会设P（x，x²+x﹣2），然后用x表示出PE、BD的长度，再根据PE＝OD求出x即可。三角形的面积随之求出。

第（3）问中的条件与问题：

条件1：满足（2）的结论；

条件2：M为直线BC上一点，在x轴的上方；

条件3：△BDM是以BD为腰的等腰三角形；

问题：求出点M的坐标

D点的坐标在第二问中已经求出，则BD的长度很容易求得，分情况讨论① BD=BM，利用y_M＝BMsin∠ABC求得M点坐标；②BD=DM，利用等腰三角形三线合一的性质以及求得M点坐标。

我们来思考，在解决问题的过程中用了哪些解题方法和数学思想？第（2）问主要利用点的坐标的意义表示线段的长度，从而求出线段之间的关系．第（3）问利用三角函数和等腰三角形的性质，以及点的坐标与线段长度之间的关系，从而求出点的坐标。第（3）问主要用到分类讨论和数形结合的思想，正是这些思想把复杂的数学问题变得简单，让数学充满着探索之美。

最后几位老师进一步对以上两个问题进行了讨论,充分挖掘题目内涵，探究出题思路。

本次活动从教师的专业发展出发，充分体现了两位数学老师的专业素养与数学讲题能力，同时在思维碰撞中进一步提高对中考压轴题的分析与预测能力。

撰稿：秦紫薇